www.中文字幕久久久,日韩精品久久久,内地老熟女老少配视频

概率理論的基本元素是某一過程的獨立結(jié)果，如一次實驗或者自然現(xiàn)象。每一個可能發(fā)生的稱為事件。每一個獨立結(jié)果被稱為基本事件。例如當完成一次訂單時，兩種可能的結(jié)果是正確完成訂單和不正確的完成訂單。每一個可能結(jié)果代表了一個基本事件。當扔一個標準的六面體骰子，骰子六個面分別有1,2,3,4,5,6個點，此時有六種可能的基本事件(見圖1)。一個事件可以是這六個基本事件中的任何一個，一組或者基本事件的子集。例如，出現(xiàn)偶數(shù)個點的事件有三個基本事件組成——2, 4或者6。

什么是概率？

圖1 一個骰子的六個面

有三種不同的方法來計算事件發(fā)生的概率：經(jīng)典方法,經(jīng)驗方法(對稱相對頻數(shù)方法)和主觀方法。

計算概率的主觀方法是基于對總體的預(yù)先了解的知識。經(jīng)典方法常常假設(shè)所有基本事件是等概率發(fā)生的。如果假設(shè)成立的話，P(A)為特定事件發(fā)生的概率，其被定義為:

事件A發(fā)生概率=A可能發(fā)生的方式數(shù)目/基本事件的總數(shù)

什么是概率？

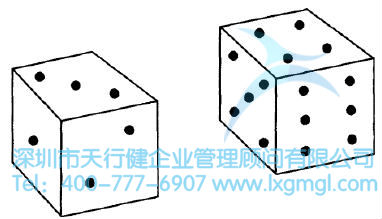
圖2 經(jīng)典概率方法

圖2說明了經(jīng)典概率方法。如果只扔一次骰子，出現(xiàn)點數(shù)為三的面的概率為1/6。在六個可能出現(xiàn)的面里只有唯一一個面有三個點。在經(jīng)典方法中，假設(shè)扔骰子過程是完全隨機且無記憶的，因此在每次扔的過程六個面出現(xiàn)的概率是相同的。因此，從長期來看，假設(shè)扔的過程是正確的，當扔6000次時從理論上我們可以假設(shè)出現(xiàn)三點的面的次數(shù)是：

1000(1/6×6000)

計算概率的實驗方法描述如下：

如果多次(如M次)重復(fù)一個實驗，那么事件A發(fā)生的概率是用實驗中A發(fā)生的次數(shù)除以M, M也為實驗中事件A可能發(fā)生的最大次數(shù)。

例如，假設(shè)在處理銀行貸款業(yè)務(wù)中，一項對最近500個貸款申請的研究顯示，遺漏貸款申請的次數(shù)為12次。結(jié)果，遺漏貸款申請的相對頻數(shù)概率如下:

P(遺漏貸款申請)=12/500=0.024

一些分析研究被用來判定過程特征。然而，過程特征都有一個過去、現(xiàn)在和未來。因此，沒有結(jié)構(gòu)可以用來計算經(jīng)典概率。涉及過程特征的概率都必須由實驗決定。且都必須是相對頻數(shù)概率。例如，一名新雇用的員工被要求從事管理工作，負責(zé)將數(shù)據(jù)從銷售表輸入到計算機終端上。該員工每小時輸入錯誤比例是否可以預(yù)測呢？答案當然是否定的。你所能采取的最好行動是對該員工進行合適的培訓(xùn)，進而觀察其長期的工作表現(xiàn)情況。如果一名員工的表現(xiàn)呈現(xiàn)出穩(wěn)定的規(guī)律，就可以計算出每小時輸入錯誤銷售表單相對頻數(shù)，來估計輸入錯誤銷售表單的概率。也可以用此相對頻數(shù)概率來預(yù)測每小時輸入錯誤的銷售表比例。

計算概率時經(jīng)典方法和實驗方法并不總是可行的。在許多情況下，當缺少計算相對頻數(shù)的基本事件數(shù)目或者實際數(shù)據(jù)時，常常使用主觀方法。主觀概率可以是基于專家判斷，或者來自于感覺與預(yù)感。如果說過程和知識為基礎(chǔ)的經(jīng)典方法和觀察數(shù)據(jù)為基礎(chǔ)的實驗方法是客觀方法的話，當個體使用不同方式來判斷一個事件的可能結(jié)果時，使用計算概率的主觀方法。不同個人對未來的交通方式、明天的天氣情況或者未來的經(jīng)濟形式可能都會有著不同的看法。